Gaussian-Process Factor Analysis (GPFA)
GPFA extracts low-d latent trajectories from noisy, high-d time series data. It combines linear dimensionality reduction (factor analysis) with Gaussian-process temporal smoothing in a unified probabilistic framework. GPFA is particularly useful for exploratory analysis of spike trains recorded simultaneously from multiple neurons on individual experimental trials.
Matlab code (version 2.03, 119 kB)
References: Yu et al., J Neurophysiol, 2009; Churchland et al., Nat Neurosci, 2010
DataHigh

DataHigh is a Matlab-based graphical user interface to visualize and interact with high-dimensional neural population activity. DataHigh has built-in tools to perform dimensionality reduction on raw spike trains, and includes a suite of visualization tools tailored for neural data analysis.
Reference: Cowley et al., J Neural Eng, 2013
Time-Delay Gaussian-Process Factor Analysis (TD-GPFA)
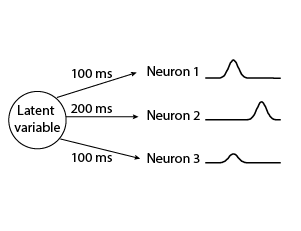
TD-GPFA is an extension of GPFA that allows for a time delay between each latent variable and each neuron. This is useful when the same latent variable describes the activity of different neurons after different time delays. As a result, TD-GPFA can be used to extract a more compact latent representation than GPFA.
This code pack also includes an updated version of GPFA that allows for parallel computing to speed up cross-validation.
Matlab code (version 3.00, 657 kB), GitHub page
Reference: Lakshmanan et al., Neural Comput, 2015
Internal Model Estimation (IME)

IME estimates the subject's internal forward model of the relationship between the recorded neural activity and cursor movement. The inputs are the recorded neural population activity and the movement goal. The outputs are a linear forward model (model parameters), and an estimate at each time point of where the subject thinks the cursor is (latent variables).
References: Golub et al., ICML, 2013; Golub et al., eLife, 2015
Distance Covariance Analysis (DCA)
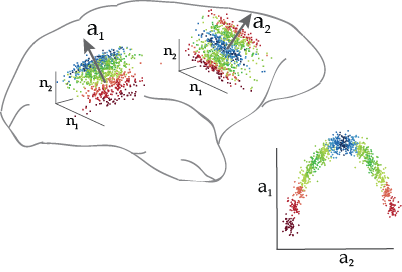
DCA is a linear dimensionality reduction method that can identify linear and nonlinear relationships between multiple data sets. For example, DCA can identify dimensions of population activity in different brain areas that are related to one another and to stimulus or behavioral variables.
Matlab code (version 1.0, 30 kB)
Python code (version 1.0, 30 kB)
GitHub page
Reference: Cowley et al., AISTATS, 2017
Neural Reassociation
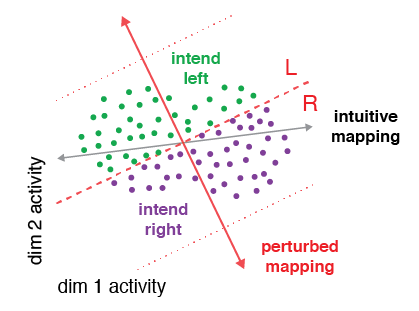
This code implements five different hypotheses — Realignment, Rescaling, Reassociation, Partial Realignment, Subselection — of how neural population activity changes with learning. The inputs are the before-learning population activity, along with the BCI mappings. The outputs are predictions of after-learning population activity according to each hypothesis.
Reference: Golub et al., Nat Neurosci, 2018
Neural Redundancy
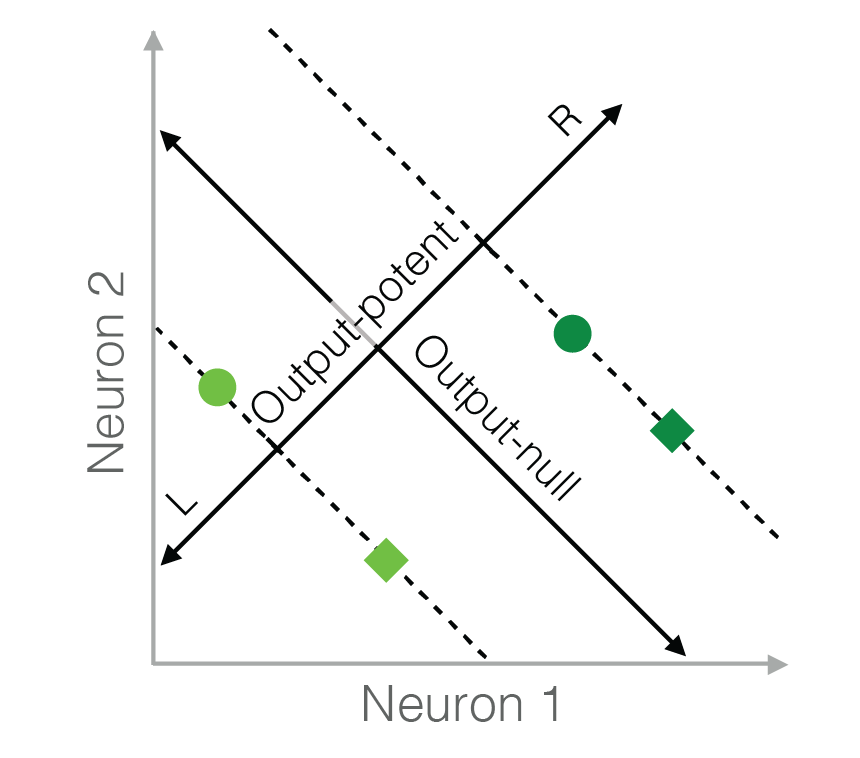
This code implements six different hypotheses of neural redundancy — Minimal Firing, Minimal Deviation, Uncontrolled-uniform, Uncontrolled-empirical, Persistent Strategy, and Fixed Distribution. The input is the activity in the output-potent space (i.e., behavior), and the output is the predicted distribution of neural activity in the output-null space according to each hypothesis.
Reference: Hennig et al., eLife, 2018
Communication subspace
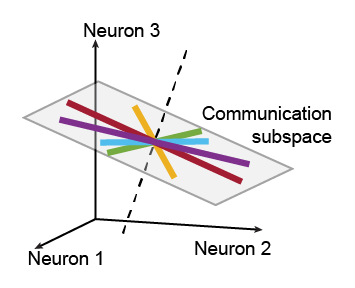
This code implements reduced-rank regression for identifying a communication subspace between brain areas. The inputs are spike counts recorded simultaneously from two populations of neurons, one population per brain area. The code assesses whether a communication subspace is present and, if so, identifies the communication subspace in the source brain area.
Reference: Semedo et al., Neuron, 2019