Error Prediction Models and Field Data

Carnegie Mellon University
Spring 1998

Michael Collins

Abstract:

Lifecycle prediction is an important part of product design, as it provides estimates for a product's safe lifetime. The need for accurate prediction schemes has resulted in various reliability prediction models which are used to qualitatively estimate the lifetimes of mechanical and electronic systems. These models are effectively 'best guesses', and to work with any degree of accuracy, they must use empirically acquired field data. We discuss several prediction models, their associated field data, and the differences between these data models.

Related Topics:

• Life Cycle
• Case Studies
• Traditional Reliability
• Project Page

Contents:

• Introduction
• Key Concepts

• Prediction Model Mathematics
• Acquiring Field Data
• Limitations
• Economics

• Available tools, techniques, and metrics
• Relationship to other topics
• Conclusions
• Annotated Reference List
• Loose Ends

Introduction

In order to predict the failure rate of a system, the Military and other organizations have developed error prediction models. These models are systematically derived equations which, by modeling properties of a system, generate predictions as to the life of the system. While they are not necessarily a perfectly accurate estimate of the lifespan of a system, these models provide an adequate initial guess and can be valuable when used by a sufficiently cautious engineer.

In order to determine meaningful failure rates, prediction models depend on observed lifetime data. There are several means of acquiring lifetime data for a system such as artificially stressing a system, initial laboratory tests and the like. Most data sources have some sort of bias, and the historic military preference has been for field data: information acquired by observing the lifetime of components in their normal use.[EPRD-97]

Prediction models depend on this data for several reasons. First, the prediction formulae are themselves derived from field data, without some idea of the natural lifespans of the components, talking about their estimated lifespans is meaningless. Second, engineers building new components plug existing field data into their derived prediction models to make an estimate. Field data is one of a group of datatypes that can be used, but it is usually the most thorough.

The standard for prediction models is the MIL-HDBK-217, an extensive handbook on various error prediction models for different systems. The MIL-217 specifications are extensive, but are also suited for a specific mode of behavior. The safety standards used by the military are not necessarily appropriate for other industries, where models of use and the consequences of failure are radically different. While the MIL-217 specification serves as the basis for almost every other prediction model, different industries have built different models to accommodate their specific needs.

Acquiring field data is a relatively onerous task: by definition, field data is gathered by observing parts fail in situ. A well designed part is less likely to have a long life time, leading to extended waiting time for any useful information. Because the task is so time consuming, there are relatively few sources, usually from the manufacturers themselves. The largest repositories of field data are the NPRD-95 and EPRD-97 produced by the military and these were the of years of observation, repair records, and other activities. Given the amount of time it takes to build such a record, these reliability tables are likely to remain the standard for years to come.

In the past twenty years, the military has become a less important client for engineering companies, and consumer products have come into a higher demand. A consequence of this change in demand has been a lessening of the MIL-217's role in reliability prediction. In general, the 217 model is considered to be considered somewhat 'pessimistic' - that the lifetime estimates are too conservative or too general. In response to these demands, industries are developing alternatives such as Bellcore TR-332 error prediction model [Relex].

Key Concepts

Acquiring and using field data is an empirical science. Most of the key concepts associated with analyzing this data are shared by any experimental discipline. A knowledge of statistical interpretation and an understanding of systematic error sources are a basic requirements.

• Mathematical Models:

  The prediction models used by the military and industry are generally based on the MIL-HDBK-217 specification. The MIL-217 uses two types of models: the parts count model and the parts stress model. In general, the parts count model is a simpler form and requires less data - it is also less accurate. The parts stress model is a more accurate estimate of lifespan, but requires considerably more parts information and is more difficult to calculate [Mil-217]. Bellcore's system apparently uses a variety of different models to calculate different results [Relex].

  None of these models are theoretically elegant; rather, they are produced by fitting curves to existing data. As an example, he standard prediction model for the auto industry is provided below [SAE84]:

  

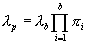
  In the above equation, Lambda_p is the predicted failure rate, Lambda_b is the base failure rate for the component, and Pi_i are various modifying factors, such as component composition, ambient temperature and location in the vehicle.

  Like most failure prediction models, this equation is based on similar equations in the MIL-217. The major difference is semantic: the modifying factors for the part are based on issues specific to the auto industry. These factors include an emphasis on generic components and the physical composition of the part. [SAE87]

• Data Acquisition: The EPRD-97 lists a variety of data sources for its field data, examples of them include the following:
  • Observed Failure Rates
    
  • Manufacturer Records
    
  • Repair Records
    
  Obviously, acquiring this data is a time consuming task, and industries will only pay attention to field data for components that directly affect them. The military is the only organization with the manpower to compile a general resource like the EPRD or NPRD.[EPRD-97]

  Because of the difficulty of acquiring field data, commercial users have started to work with alternate data sources to calculate error rates. These data sources include:

  • Laboratory Experiments
    
  • Environmental Stress Testing
    
  Unlike the factors above, these factors are 'artificial', in the sense that the experimenter introduces conditions to instigate failure, rather than waiting for failure to happen.

• Limitations Of Field Data: The answers derived by prediction models are not accurate for several reasons:
  • The prediction models are best guesses.

  • Accurate data is hard to come by.

  • It is entirely possible to find components with no field data.

  As an example, look at the following data culled from the EPRD-97. These failure rates for for silicon 74LS251`transistors from various manufacturers.

  Source	Failure Rate
  GBC 13567-008	2/22.9840E6
  GBC 13567-013	3/34.8452E6
  GBC 13567-012	1/58.6820E6
  GBC-13567-010	6/41.4401E6

  Assuming for now that the results are hour-based (The EPRD-97 isn't clear on a part by part basis), then these figures have a mean failure of 8.3735+/-7.3543 Errors / 10,000 Hours.

  Because of the uncertainty in failure rates and the (potential) inaccuracy in rate prediction models, a safety-minded designer must engineer conservatively. This point is stressed in the EPRD-97, engineers are encouraged to use the in-depth data whenever possible, instead of using the mean values. Other techniques (such as cutting the estimated lifespan by a factor of two or more), are already common practice for safety minded engineers. Error prediction rates are intended as a complement for safety minded design, not a substitute.

• Industry Specific Models:Prediction models are usually driven by the concerns of an industry. Military/Aerospace prediction stresses reliability over long periods, while automotive reliability is based on an estimate of 400 hours of use per year. Industries build failure models which complement their needs, and those needs drive the requirements on field data.

  In this respect, the MIL-217 serves as a starting point: new models are formed using the MIL-217 formulae, usually using the same form but introducing new correction factors. The economic requirements of an industry will affect the prediction models, and consequently the reported field data for several reasons: first, gathering data is an expensive process and there are very few customers who need a generic field data source. Second, since the error prediction models look for different corrective factors (such as component placement), the field data gathered will focus on those factors and ignore others. Airplanes are not cars, tanks are not relays, and industries try to accommodate these differences in their failure models.

  For example, note the emphasis on generic parts in the SAE model. Given the variability of error rates discussed above, generic parts would seem inadvisable. However, the values given in the EPRD-97 are calculated over 100,000 hours, while the automobile industry expects the average car to operate for 400 hours a year. Using the average transistor failure rate derived above (8.3735+/-7.3543 Errors / 10,000 Hours), automobiles should encounter 0.33494 transistor errors per year, or about 1 error every three years. Although this is a rough estimate, it provides an indication of why the MIL-217 model may be considered inappropriate.

  Failure prediction models will emphasize or de-emphasize data based on the model's purpose. The best way to illustrate this is to compare the MIL-217 and SAE's model. As noted above, the EPRD-97 prediction data places an emphasis on the sources for the data, but stops there. Unlike the military model, the SAE model uses average values for their data sources to guarantee confidentiality [SAE87]. However, unlike the MIL-217 model, the SAE prediction formulae calculate field data for various environmental factors in the vehicle: location, heat sources, electrical interference and so on. These mitigating factors are another form of field data, since they are gathered empirically and converted into multiplicative factors for the prediction models.

Available tools, techniques, and metrics

Formalized error prediction began with the MIL-217 and the bulk of failure prediction tools are based around making the MIL-217 more tractable. Examples include:

• MILStress allows users to build hierarchical models of systems and then apply the MIL-217 failure rates. It also includes libraries of parts data culled from the EPRD and other sources.
  
• Relex is an expandable reliability calculator. Relex provides support for both the Bellcore and 217 models.

As the MIL-217 becomes less important, many of these tools include the TR-332 as an alternative system. There are a number of products which handle both models, and include conversion facilities.

The other major tool are the data sources: the NPRD-95 and EPRD-97 error rate repositories. These books are published by the U.S. Reliability Analysis Center and are nothing more than giant compendia of failure rates. The EPRD and NPRD are extremely detailed work; as noted above, their failure data may be too detailed for a particular industry. Certain industries have developed smaller compendia for their own purposes.

Relationship to other topics

• Life Cycle. Error prediction models provide borders for the life cycle, telling how long a product is expected to last.

• Case Studies. Case studies are another case of drawing current engineering knowledge from past failures. However, error prediction models, unlike case histories, are a more qualitative topic. Case studies tend to focus on more nebulous design concerns, while reliability models are concerned with acquiring actual numbers.

• Traditional Reliability Technically, field data and prediction models are associated with all the reliability topics. However, prediction models were first designed for mechanical systems, and to a large extent, the reliability model espoused by MIL-217 is still based around the traditional, mechanical definitions of reliability.

Conclusions

While basically a mathematically based guess, formal error prediction is a necessary part of safety-centered design. Error prediction models provide estimates on the lifetime of systems, and serve as a starting point for determining the realistic lifespan of a system.

Error prediction drives the need for field data on failure rates. Field data can be gathered from a variety of sources, each of whom may introduce systematic error into the prediction model. Some knowledge of experimental methods, such as statistical analysis and sources of systematic error, can help turn the raw data into meaningful values.

The basis for error prediction models is the MIL-HDBK-217, a military compendium developed in the late 1940's and periodically updated since. The MIL-217 is an extensive and generalized source and consequently may not be appropriate for all industries. As with many other disciplines the MIL-217 prediction model is suffering from the peace dividend. As the military becomes a less important customer, alternative models which place more of an emphasis on consumer needs become more attractive.

Annotated Reference List

• [MIL217] MIL-HDBK-217
  The "217" is the military's failure prediction handbook, revised regularly since the 1950's. The 217 handbook is the basic text on failure prediction, the mathematical models derived in the book are the basis for all other prediction models.

• [EPRD97] EPRD-97
  The EPRD-97 is a handbook containing failure rates for electronic components. The EPRD-97 is an extremely in-depth publication, containing failure rates for specific makes and models of various components.

• [SAE84] Binroth, Coit, Desnon and Hammer. "Development Of Reliability Prediction Models For Electronic Components In Automotive Applications", SAE Paper 840486.
  This paper introduces the SAE reliability prediction model. In addition to explaining the model, it provides insights into why the SAE would need a model distinct from the 217 specification.

• [SAE87] Denson and Priore. "Automotive Electronic Reliability Prediction", SAE Paper 870050.
  This paper refines the model developed in [SAE84] with further empirical evidence and reformulations. The commentary on heat factors gives a good example of how reliability factors are developed and calculated.

• [Relex] Relex Software Website.
  Relex is a good example of a company producing reliability prediction tools. While their site is obviously biased towards their product, they are selling reliability calculation tools, not reliability models themselves.

Loose Ends

I wasn't really able to say that much about the Bellcore model for financial reasons: actually purchasing a copy of the Bellcore model is outside of my means right now.

One interesting point is that the Bellcore model's rise is a result of the peace dividend: as the military becomes a less important customer, the military reliability standards become less important. It would be interesting to provide exact specifications for how the Bellcore model differs as a consequence. I've touched on some of this by discussing the SAE's emphasis on generic parts - legal issues require them to use generic parts, rather than finger individual customers. Bellcore apparently extends these kind of concerns in other directions - using field testing data, for example.

Go To Project Page