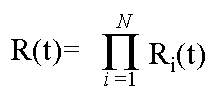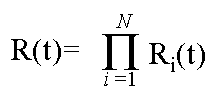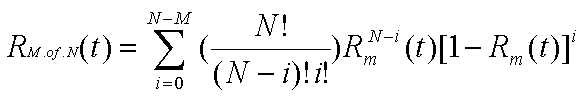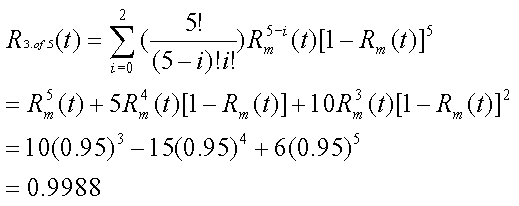Traditional Reliability
Carnegie Mellon University
18-849b Dependable Embedded Systems
Spring 1998
Author: John DeVale
Abstract
The multi-disciplinary nature of embedded systems demand an all encompassing
approach to reliability, requiring consideration of traditional (hardware)
reliability, as well as software and mechanical reliability. Traditional
hardware based reliability is a well understood, amply researched area.
Mature fault models provide system designers with good theoretical tools
to determine overall system reliability. Fault handling techniques provide
a robust methodology by which highly reliable system can be built. Mathematical
models for serial and parallel design allow the construction of highly reliable
systems, while n-version redundancy techniques helps to tolerate errors
injected into the system during the design phase.
Contents
Introduction
Equipment reliability problems which occurred during the second World
War is widely believe to be the impetus for the development of the study
of reliability [storey96]. Realizing that defense technology would become
increasingly complex, and reliant on electrical and electronic components,
the US Department of Defense initiated projects to study the field of reliability.
As our ability to model systems and predict reliability grew, so too did
our ability to build reliable systems.
One of the first to delve into reliability research was the well known
German Rocket Engineer Wernher Von Braun. During World War II, Von Braun
and his team developed first the V-1 rocket (also known as the Buzz-Bomb)
and later the V-2 rocket. The V-1 rocket was plagued with reliability problems.
Von Braun and his team worked to fix it. They used ideas stemming from simple
mechanical reliability (i.e. if you fix the weakest link in a chain it will
not break) to diagnose and fix the rocket. When Von Braun and his team made
the least reliable part more reliable, they discovered that the V-1 was
still 100% unreliable [vilmer].
Eric Pieruschka, a German mathematician working with Von Braun on a different
project, was able to help Von Braun with his reliability troubles. Pieruschka
pointed out to Von Braun that his reliability model was incorrect. Von Braun
assumed that the rocket would be as reliable as the least reliable part.
Pieruschka showed Von Braun that the rocket’s reliability would be
equal to the product of the reliability of its components, and was
the first documented modern predictive reliability model. This result formed
the basis for what later became know as Lusser’s law: |
 |
Rs=R1 x R2 x … x Rn
A more modern formulation of system reliability expressed as:
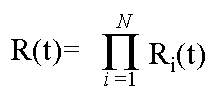
Since is beginning, massive amounts of work has been done in the field
of reliability, with many volumous scholarly tomes written on only small
aspects of what we consider traditional reliability. This brief introduction
will attempt to familiarize the reader with the basics of traditional reliability,
and how it relates to the other topics in this text. Other chapters will
delve deeply into specific aspects of reliability as it relates to embedded
systems.
Key Concepts
Definitions
In order to communicate effectively in any field, it is important to
known the terms associated with it. This is especially true in reliability,
where different people use the terms in similar, but slightly different
ways. For the purposes of this text, we will use the terms as defined by
Siewiorek and Swarz in [Siewiorek92].
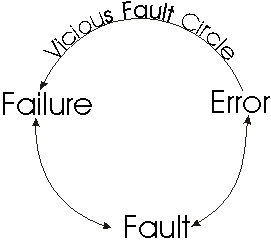
Failure
A failure occurs when the service delivered by a system fails to meet
its specification; caused by an error.
Fault
A fault is an incorrect system state, in hardware or software, resulting
from failures in system components, design errors, environmental interference,
or operator errors.
Error
An error is the manifestation of a system fault. For example, an operator
enters the wrong account number to be canceled in the power company computer
(fault). The system then shuts off power to the wrong node (error).
Permanent
A permanent fault or failure is one which is stable and continuous. Permanent
hardware failures require some component to be replaced or repaired. An
example of a permanent fault would be a VLSI chip with a manufacturing defect,
causing one input pin to be stuck high.
Intermittent
An intermittent fault is one which only manifests occasionally, due to
unstable hardware or certain system states. For instance most microprocessors
do not perform data forwarding errors correctly for certain sequences of
instructions (injecting a fault in data). As these are discovered, developers
add code to compilers to prevent them from generating those specific sequences.
Transient
A transient fault is one which results from a temporary environmental
condition. For example, a voltage spike might cause a sensor to report an
incorrect value for a few milliseconds before reporting correctly.
| Consider a computer controlled power plant, in which the system is responsible
for monitoring various plant temperatures, pressures, and other physical
characteristics. The sensor reporting the speed at which the main turbine
is spinning breaks, and reports that the turbine is no longer spinning.
The failure of the sensor injects a fault (incorrect data) into the system.
This fault causes the system to send more steam to the turbine than is required
(error), over-speeding the turbine, and resulting in the mechanical safety
shutting down the turbine to prevent damaging it. The system is no longer
generating power (system failure). Now other systems relying on power from
the system have faults, in the form of inadequate power, and may in turn
fail, and cause other failures as a result. |
 |
Development
Stages and Faults
Faults can be injected at any stage of the design and manufacturing process.
Figure X shows the various stages of a simplified development cycle, what
types of faults are typically injected during each stage, and effective
error detection techniques (remember that errors are manifestations of faults)
[siewiorek 92].

Fault Handling
Although we might like to have all the bugs worked out of our systems
before they go into the field, history tells us that such a goal is not
attainable. It is inevitable that some environmental factor will not be
considered, or some potential user error will be completely unexpected.
Thus even in the unlikely case that the system was implemented perfectly,
faults will likely be injected by situations out of the control of the designers.
A reliable system must be able to handle unexpected faults and still
meet service specification. Four general groups have been identified which
loosely classify techniques for building reliability into a system [storey96
siewiorek92]. These are fault avoidance, fault detection, masking redundancy,
and dynamic redundancy [siewiorek92], or fault avoidance, fault detection,
fault removal, fault tolerance [storey96]. While the last two groups are
not identical between references, they are similar, and encompass the same
techniques, but in different groups. For our purposes we will use the groups
as laid out in [siewiorek92].
Fault Avoidance
Fault avoidance techniques are intended to keep faults out of the system
at the design stage. These might include a rigid software development process
or formal verification techniques [storey96].
Fault Detection
These techniques try to detect faults within an operating system. Once
the faults are detected, other techniques will be applied to correct the
fault, or at least minimize its impact on the service delivered by the system
[storey96]. Such techniques include error detection codes, self-checking/failsafe
logic, watchdog timers, and others [siewiorek92].
Masking Redundancy
These techniques prevent the system from being affected by errors by
either correcting the error, or compensating for it in some fashion. This
includes techniques such as error correcting codes, interwoven logic, algorithmic
diversity [siewiorek92].
Dynamic Redundancy
Techniques that attempt to use existing system resources to work around
a fault fall under this classification. This includes a wide array of techniques
including retry, checkpointing, journaling, n-modular redundancy, reconfiguration
and graceful degradation.
A good reliable system may need to use multiple techniques from each
category to meet its reliability goals.
System
Failure Response Stages
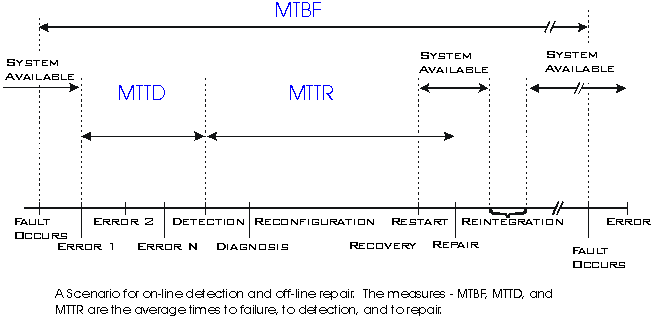
Once a fault has been injected into a system, the system may go through
as many as eight distinct stages to respond to the occurrence of a failure
[siewiorek92]. While a system may not need, or be able to use all 8, any
reliable design will use several, coordinated techniques. The stages are:
fault confinement, fault detection, diagnosis, reconfiguration, recovery,
restart, repair, and reintegration. Each stage is discussed briefly below.
Fault containment
The purpose of this stage is to limit the spread of the effects of a
fault from one area of the system into another area. This is typically achieved
by making liberal use of fault detection (early and often), as will as multiple
request/confirmation protocols and performing consistency checks between
modules.
Fault detection
This is the stage in which the system recognizes that something unexpected
has occurred. Detection strategies are broken into two major categories,
online detection and offline detection. A system supporting online detection
is capable of performing useful work while detection is in progress. Offline
detection strategies (like a single user diagnostic mode) prevent the device
from providing any service during detection.
Diagnosis
If the detection phase does not provide enough information as to the
nature and location of the fault, the diagnosis mechanisms must determine
the information. Once the nature and location of the fault have been determined,
the system can begin to recover.
Reconfiguration
Once a faulty component has been identified, a reliable system can reconfigure
itself to isolate the component from the rest of the system. This might
be accomplished by having the component replaced, by marking it offline
and using a redundant system. Alternately, the system could switch it off
and continue operation with a degraded capability (similar to the way the
Hubble Space Telescope was reconfigured to compensate for a faulty mirror
until it could be replaced). This is known as "graceful degradation."
Recovery
In this stage the system attempts to eliminate the effects of the fault.
A few basic approahces for use in this stage are fault masking, retry, and
rollback.
Restart
Once the system eliminates the effects of the fault, it will attempt
to restart itself and resume normal operation. If the system was completely
successful in detecting and containing the fault before any damage was done,
it will be able to continue without loss of any process state. This is known
as a "hot" restart. In a "warm" restart, only a few
processed will experience state loss. In a "cold" restart, the
entire system looses state, and is completely reloaded.
Repair
During this stage, any components identified as faulty are replaced.
As with detection, this can be either offline or online.
Reintegration
The reintegration phase involves placing the replaced component back
in service within the system. If the system had continued operation in a
degraded mode, it must be reconfigured to use the component again, and upgrade
its delivered service.
Reliability Models
Once research began, scientists rapidly developed models in an attempt
to explain their observations on reliability. Mathematically, these models
can be broken down into two classes, parallel reliability and serial reliability.
More complex models can be built by combining the two basic elements of
a reliability model.
Serial Reliability
Many systems perform a task by having a single component perform a small
part of it, and pass its result to another component in a serial fashion.
The new component then performs a small piece of the task, and continues
passing it along, until the task is completed. This is how people typically
design programs, and hardware devices. The solutions can be cost effective
and elegant.
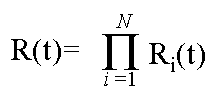
As Von Braun discovered, this makes it exceedingly difficult to built
a reliable system. Such systems can have their reliability modeled using
the following equation:
Thus building a serially reliable system is extraordinarily difficult
and expensive.
For example, if one were to build a serial system with 100 components
each of which had a reliability of .999 the overall system reliability would
be 0.999100 = 0.905.
Parallel Reliability

By utilizing redundancy, system component, hardware or software (provided
the algorithms are diverse) can provide a boost in reliability. In the simplest
case (fail silent components no correctness voting) only one of the redundant
components must be working to maintain the system’s level of service.
This is characterized by the following equation:
Consider a system built with 4 identical modules. The system will operate
correctly provided at least one module is operational. If the reliability
of each module is .95, then the overall system reliability is:
1-[1-.95]4 = 0.99999375
In this way, reliable system can be built despite the unreliability of
its component parts, though the cost of such parallelism can be high.
Combinational
System Reliability
Models of more complex systems may be built by combining the simpler
serial and parallel reliability models. Consider the following system of
components:
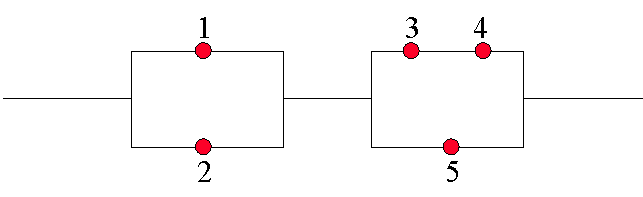
We first introduce a new term, which is useful when considering such
combinational systems.
Minimal
Set Path
A minimal path set is the smallest set of components whose functioning
ensures the functioning of the system [ross97]. In this case it is {1,3,4}
{2,3,4} {1,5} {2,5}.
The total reliability of the system can be abstracted as the reliability
of the first half, in serial with the reliability of the second half.
Given that R1=.9, R2=.9, R3=.99, R4=.99, R5=.87
Rt=[1-(1-.9)(1-.9)][1-(1-.87)(1-(.99*.99))] =.987.
Such a system might be built if 5 was extremely fast, but not very reliable.
Components 3 and 4 are reliable but slow. So the system can race along using
5 until it fails. System service degrades until 5 can be reset and reintegrated
into the system.
Component
Reliability Lifetime Model
During useful life, a physical electronic component typically has a constant
failure rate, and its reliability is statistically represented as:
R(t) = e-lt
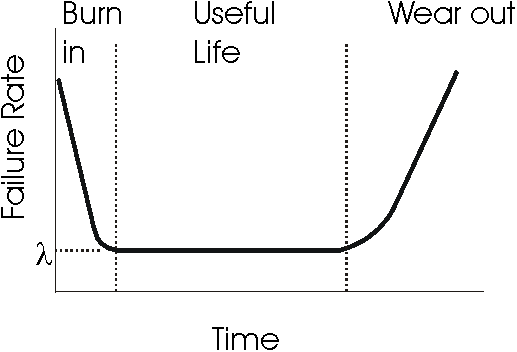
Over the part’s lifetime, its reliability looks somewhat different
[storey96]:
The high failure rate during the burn in period accounts for parts with
slight manufacturing defects not found during manufacture’s testing.
N-version
Modular Redundancy
One of the classic methods for improving reliability, n-version modular
redundancy can be very effective when implemented correctly. It is also
extremely expensive to do so. Typically only the most mission critical system
will employ n-version modular redundancy, such as are found in the aerospace
industry.
The fundamental idea behind n-version modular redundancy is that of parallel
reliability. These systems can also compensate for correctness issues stemming
from faults injected during the design and specification phases of a project.
The independent modules all perform the same task in parallel, and then
use some voting scheme to determine what the correct answer is. This voting
overhead means that n-modular redundant systems can only approach the theoretical
limit of reliability for a fully parallel reliable system.
The reliability of an n-modular redundant system can be mathematically
described as follows:
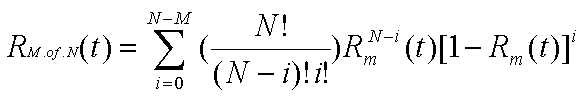
Where N is the number of redundant modules, and M is the minimum number
of modules required to be functioning correctly, disregarding voting arrangement.
Consider a 5 module system requiring 3 correct modules, each with a reliability
of 0.95 [storey96].
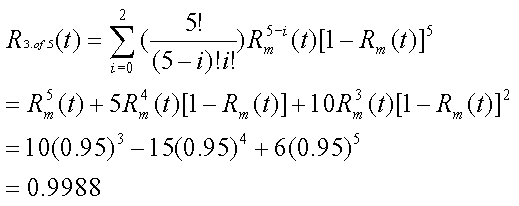
Relationships
to other Areas
Traditional reliability spans years or research and enormous volumes
of work. There is almost no aspect of building reliability that is not affected
by it in some way. The strongest connections are listed here, to facilitate
the inference of connections in later parts of the text.
Related Topics
Related Clusters
Conclusions
The following ideas are the most important to understand from this topic:
- It is important to define terms the way one uses them. Other practitioners
of reliability use many of them interchangeably or differently.
- The common techniques for fault handling are fault avoidance, fault
detection, masking redundancy, and dynamic redundancy.
- Any reliable system will have its failure response carefully built
into it, as some complementary set of actions and responses.
- System reliability can be modeled at a component level, assuming the
failure rate is constant (exponential distribution).
- Reliability must be built into the project from the start.
Annotated References
| [Ross97] |
Ross, Sheldon M., Introduction to Probability Models, 6th Edition, 1997,
Academic Press
This textbook introduces elementary probability and stochastic processes.
Chapter 9 is devoted to reliability theory and models. |
| [Siewiorek92] |
Siewiorek, D.P., Swarz, R.S., Reliable Computer Systems - Design and
Evaluation, 2nd Edition, 1992, Digital Press
Perhaps the cannonical text on the subject, the authors provide a comprehensive
guide to the design, evaluation and use of reliable computing systems. |
| [storey96] |
Storey, Neil., Safety-Critical Computer Systems, 1996, Addison-Wesley
Longman
This is a very complete work which describes methods and pitfalls when
building safety critical systems. |
| [villemeur] |
Villemeur, Alain., Reliability, Availability, Maitainability and Safety
Assesment: Volume 1 - Methods and Techniques, 1992, Wiley and Sons
This work contains a huge amount of information on reliability and safety.
Very complete. |
devale@cmu.edu 03/23/99 21:56