BiBa Extensions

 

The first way to increase the security is to increase the number of SEALs and bins, but that approach would increase the size of the public key.

  
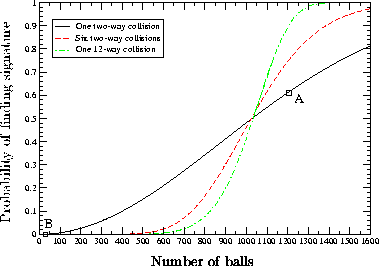
Figure 2: Probability of finding a signature for three cases. The solid line shows the probability for finding a two-way collision when throwing $x$ balls into $762460$ bins. The dashed line shows the probability of finding six two-way collisions when throwing $x$ balls into $236650$ bins. The dot-dashed line shows the probability of finding a six-way collision when throwing $x$ balls into $222$ bins. We selected the number of bins such that the signer has a $50\%$ probability of finding a signature with $1024$ SEALs after one try.

A better approach to increase the security is to use multiple two-way collisions to generate a signature. For example, a signature on message $m$, with $h=H(m)$, would consist of $z$ two-way collisions. The signature is composed of $z$ pairs of SEALs $S$a₁,Sb₁,&ldots;, Sa_z,Sb_z, with all SEALs distinct and $G$_h(Sa_i)=G_h(Sb_i) ($1\; \le i\; \le z$). Figure 2 shows the probability of finding six two-way collisions with $n\; =\; 236650$ bins, varying the number of SEALs.

The third way to increase security is to require multi-way collisions, instead of two-way collisions. If the BiBa signature requires a $k$-way collision, the BiBa signature of message $m$ (with $h=H(m)$) is $$x₁, &ldots;, Sx_k, where all SEALs $S$x₁, &ldots;, Sx_k are distinct and collide under $G$: $G$_h(S₁₇₀x₁) = &ldots;= G_h(S₁₇₂x_k). Figure 2 shows the probability of finding a six-way collision with $n\; =\; 222$ bins, varying the number of SEALs. The figure shows clearly that this approach is better than using six two-way collisions, because the probability drops off faster for an adversary that has fewer SEALS.

The fourth way we attempted to improve the security is to use a multi-round scheme, where only the bins that have a $k$₁-way collision in the first round proceed as balls into the next round. Intuitively, multi-round schemes may seem to improve the security. However, we show in Appendix A that one-round schemes are as secure as multi-round schemes.