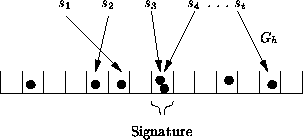
Figure 1: Basic BiBa scheme
To sign a message , the signer first computes the hash . The signer then computes the hash function (as we describe at the beginning of this section) to all the SEALs . The signer looks for a two-way collision of two SEALs: , with . The pair forms the signature. Figure 1 shows an example. It is now clear why the BiBa acronym stands for Bins and Balls signature: the bins correspond to the range of the hash function , and the balls correspond to the SEALs.
We exploit the asymmetric property that the signer has more SEALs than the adversary, and hence the signer can easily generate the BiBa signature with high probability. On the other hand, an adversary only knows the few disclosed SEALs and hence has a low probability to find a valid BiBa signature.