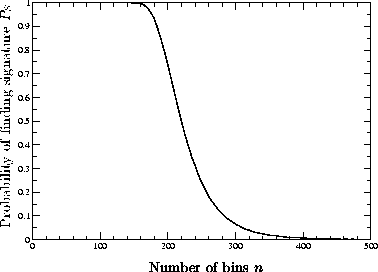
Figure 5: Probability of finding a twelve-way collision when throwing balls into bins.
We assume that the sender has SEALs. Let denote the probability that an attacker can find a signature with one trial of one message knowing at most SEALs. The security parameter is generally expressed as the expected number of hash function operations that an adversary has to perform to forge a signature [15]. For BiBa, the minimum number of hash function operations to forge a signature is , for simplicity we use .
Let denote the probability that the sender can find a signature in one trial. The expected number of tries that the sender performs to find a signature is . Without loss of generality we set .
To achieve good security, the sender can disclose approximately up to of the SEALs. Each signature reveals SEALs. The sender knows SEALs, so it can produce signatures in a time period. As we discuss in Section 3, the sender needs to wait for time until it can disclose the SEALs of the next time period. Hence it needs multiple BiBa instances, if it wants to send more than messages per time period . Given the packet sending rate , the number of BiBa instances needed is .
We now discuss how we choose and . The choice of directly determines the signature size. We can derive the number of bins from and the probability that the sender finds a signature after one trial. Figure 5 shows how decreases as we increase .

Figure 5: Probability of finding a twelve-way collision when throwing balls
into bins.
Once we fix and we can derive the number of SEALs that the sender can disclose such that the adversary has at most a probability of to forge a signature. Figure 6 depicts the probability distribution to find a signature given a certain number of SEALs. As we can see in Figure 6(a), quickly decreases as the sender decreases the number of SEALs it discloses. If is too high (insufficient security) for a -way collision, we need to increase .
![]()
Figure 6: Probability of finding a signature given SEALs. These
probabilities are for the scheme .