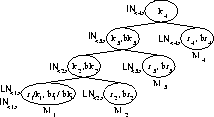
Figure 1: Notation for STR
We use the following notation:
| number of protocol parties (group members) | |
| group member indices: | |
| -th group member; | |
| 's session random (secret key of leaf node ) | |
| 's blinded session random, i.e. | |
| secret key shared among ... | |
| blinded , i.e. | |
| large prime number | |
| exponentiation base |
| Tree-specific notation | |
| Tree node | |
| Internal tree node at level | |
| Leaf node associated with member | |
| Tree of member | |
| Tree of member including all of its blinded keys | |
Figure 1 shows an example of an STRkey tree. The tree has two types of nodes: leaf and internal. Each leaf node is associated with a specific group member. An internal node always has two children: another (lower) internal node and a leaf node . The exception is which is also a leaf node corresponding to . (Note that, consequently, .)
Each leaf node has a session random chosen and kept secret by . The blinded version thereof is .
Every internal node has an associated secret key and a public blinded key . The secret key is the result of a Diffie-Hellman key agreement between the node's two children. ( is an exception and is equivalent to .) is computed recursively as follows:
The group key in Figure 1 is the key associated with the root node:
We note that the root (group) key is never used directly for the purposes of
encryption, authentication or integrity. Instead, such sub-keys are derived
from the root key, e.g., by applying a cryptographically secure hash function
to the root key. All blinded keys
The basic key agreement protocol is as follows. We assume that all members know
the structure of the key tree and their initial position within the tree. (It is
simple to have an ordering that uniquely determines the location of each member
in a key tree.) Furthermore, each member knows its session random and the
blinded session randoms of all other members. The two members
Next,
Following every membership change, all members independently update the key
tree. Since we assume that the underlying group communication system provides
view synchrony (see Section 2.1), all members who correctly
execute the protocol recompute an identical key tree after any membership event.
The following fact describes the minimal requirement for a group member to
compute the group key:
Proof.
This follows directly from the recursive definition of the group key. In other
words, both
Proof.
This also follows from the definition of the group key. To compute the group
key, member
The protocols described below benefit from a special role (called sponsor) assigned to a certain group member following each membership change. A sponsor reduces communication overhead by performing "housekeeping" tasks that vary depending on the type of membership change. The criteria for selecting a sponsor varies as described below.