What is it
Super-FFT is our unified Cooley-Tukey algorithm for all "time"-based transforms (as opposed to "space" transforms = DCTs/DSTs). Time transforms are basically real and complex DFTs of types 1-4, skew DFTs, the discrete Hartley transform, and a few others.
This work is currently unpublished, and I just provide a glimpse on this page. We are currently working on a paper.
Recursion
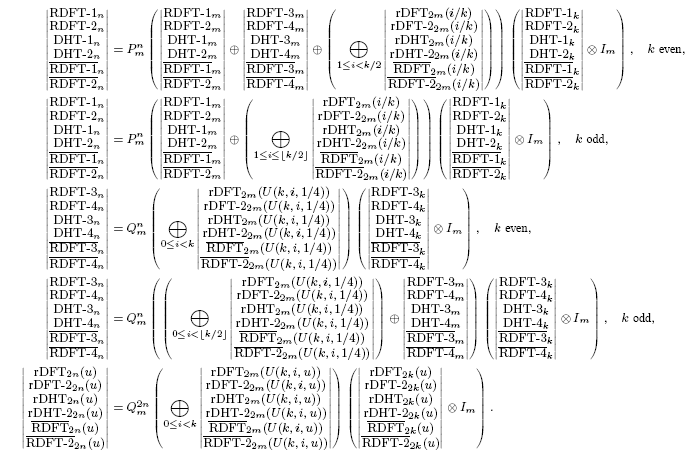
Below are the "unified" breakdown rules. Each breakdown rule covers multiple transforms. It was absolutely astounding for me to find out that all of the transforms (within a group) can be computed using the same basic algorithm. P, Q are permutations. U is a function on rationals.
Another amazing fact, is that the below recursion also covers the Bruun's FFT algorithm. Bruun's FFT is basically the recursion thru RDFT-bar. This will be explained in the paper.
Finally, the same algorithm exists for the complex DFT, but the permutation in the end becomes slightly different.
Base cases
