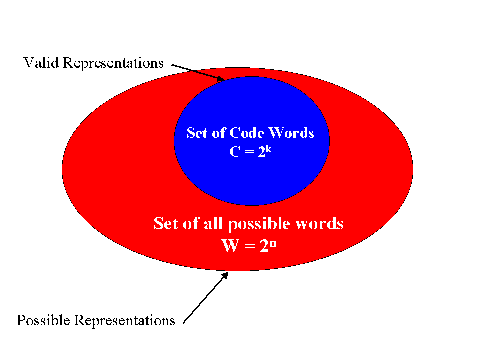
Environmental interference and physical defects in the communication medium can cause random bit errors during data transmission. Error coding is a method of detecting and correcting these errors to ensure information is transferred intact from its source to its destination. Error coding is used for fault tolerant computing in computer memory, magnetic and optical data storage media, satellite and deep space communications, network communications, cellular telephone networks, and almost any other form of digital data communication. Error coding uses mathematical formulas to encode data bits at the source into longer bit words for transmission. The "code word" can then be decoded at the destination to retrieve the information. The extra bits in the code word provide redundancy that, according to the coding scheme used, will allow the destination to use the decoding process to determine if the communication medium introduced errors and in some cases correct them so that the data need not be retransmitted. Different error coding schemes are chosen depending on the types of errors expected, the communication medium's expected error rate, and whether or not data retransmission is possible. Faster processors and better communications technology make more complex coding schemes, with better error detecting and correcting capabilities, possible for smaller embedded systems, allowing for more robust communications. However, tradeoffs between bandwidth and coding overhead, coding complexity and allowable coding delay between transmission, must be considered for each application.
Error coding is a method of providing reliable digital data transmission and
storage when the communication medium used has an unacceptable bit error rate
(BER) and a low signal-to-noise ratio (SNR). Error coding is used in many
digital applications like computer memory, magnetic and optical data storage
media, satellite and deep space communications, network communications, and
cellular telephone networks. Rather than transmitting digital data in a raw bit
for bit form, the data is encoded with extra bits at the source. The longer
"code word" is then transmitted, and the receiver can decode it to
retrieve the desired information. The extra bits transform the data into a
valid code word in the coding scheme. The space of valid code words is smaller
than the space of possible bit strings of that length, therefore the
destination can recognize invalid code words. Figure 1 illustrates the code
word space.
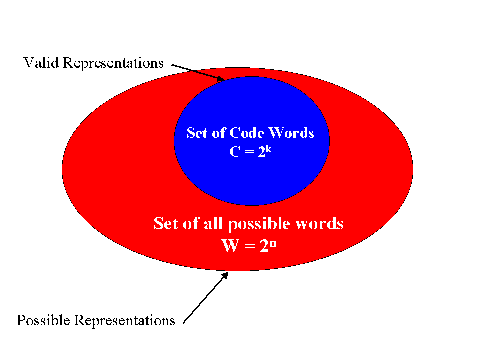
|
| |
If errors are introduced during transmission, they will likely be detected during the decoding process at the destination because the code word would be transformed into an invalid bit string. Given a data string to be transmitted that is k bits long, there are 2k possible bit strings that the data can be. Error coding assumes the worst case scenario that the information to be encoded can be any of these bit strings. Therefore there will be 2k valid code words. The code words will be n bits long, where n > k. So just having extra bits in the data transmission eliminates many of the possible 2n bit strings as valid code words.
Perhaps the simplest example of error coding is adding a parity check bit. A
bit string to be transmitted has a single bit concatenated to it to make a code
word for transmission. The bit is a 1 or a 0 depending on the parity. If odd
parity is being used, the parity bit will be added such that the sum of 1's in
the code word is odd. If even parity is being used, the sum of 1's in the code
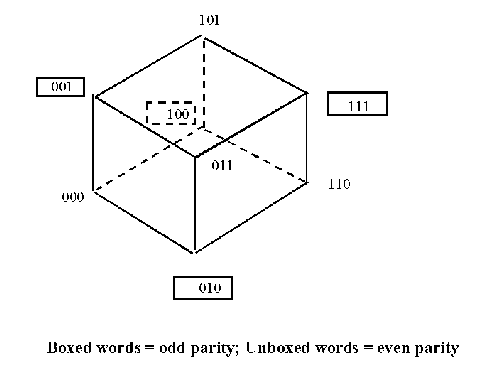
word must be even. This is illustrated in the 3-bit example in Figure 2 below.
|
| |
Here, we want to send two bits of information, and use one parity check bit for a total of three-bit code words. The data can be four possible bit combinations, so the code word space is four out of the eight possible 3-bit strings. Here we are using odd parity. When data is transmitted using this coding scheme, any bit strings with even parity will be rejected because they are not valid code words. This simple coding scheme is limited because it can only detect an odd number of bit errors from the original data, and has no error correcting capabilities. There are many other methods of error coding that provide better protection at the expense of increased bandwidth and complexity.
The error detecting and correcting capabilities of a particular coding scheme is correlated with its code rate and complexity. The code rate is the ratio of data bits to total bits transmitted in the code words. A high code rate means information content is high and coding overhead is low. However, the fewer bits used for coding redundancy, the less error protection is provided. A tradeoff must be made between bandwidth availability and the amount of error protection required for the communication.
Error coding techniques are based on information coding theory, an area developed from work by Claude Shannon. In 1948, Shannon presented a theory that states: given a code with a code rate R that is less than the communication channel capacity C, a code exists, for a block length of n bits, with code rate R that can be transmitted over the channel with an arbitrarily small probability of error. Theoretically, we should be able to devise a coding scheme for a particular communication channel for any error rate, but no one has been able to develop a code that satisfies Shannon's theorem [Wells99]. This would indicate that there is still much work to be done improving error coding techniques. Cryptography, the method of encrypting data for security rather than reliability, is also a descendant of Shannon's work.
When choosing a coding scheme for error protection, the types of errors that tend to occur on the communication channel must be considered. There are two types of errors that can occur on a communication channel: random bit errors and burst errors. A channel that usually has random bit errors will tend to have isolated bit flips during data transmissions and the bit errors are independent of each other. A channel with burst errors will tend to have clumps of bit errors that occur during one transmission. Error codes have been developed to specifically protect against both random bit errors and burst errors.
Real-time systems must consider tradeoffs between coding delay and error protection. A coding scheme with high error-correcting capabilities will take longer to decode and will be non-deterministic. This could cause a missed deadline and failure if a piece of needed information is stuck being decoded.
In embedded systems, error coding is especially important because the system may be used in critical applications and cannot tolerate errors. Coding schemes are becoming increasingly complex and probabilistic, making implementation of encoders and decoders in software attractive. Since processing power is relatively fast and cheap, software coding is more feasible. However, software is much more prone to design defects and errors, making the coding algorithm less reliable. Pushing complexity into software introduces more errors in design and implementation.
There are two major types of coding schemes: linear block codes and convolutional codes. Linear block codes are characterized by segmenting a message into separate blocks of a fixed length, and encoding each block one at a time for transmission. Convolutional codes encode the entire data stream into one long code word and transmit it in pieces.
Linear block codes are so named because each code word in the set is a linear combination of a set of generator code words. If the messages are k bits long, and the code words are n bits long (where n > k), there are k linearly independent code words of length n that form a generator matrix. To encode any message of k bits, you simply multiply the message vector u by the generator matrix to produce a code word vector v that is n bits long [Lin83].
Linear block codes are very easy to implement in hardware, and since they are algebraically determined, they can be decoded in constant time. They have very high code rates, usually above 0.95. They have low coding overhead, but they have limited error correction capabilities. They are very useful in situations where the BER of the channel is relatively low, bandwidth availability is limited in the transmission, and it is easy to retransmit data.
One class of linear block codes used for high-speed computer memory are SEC/DED (single-error-correcting/double-error-detecting) codes. In high speed memory, bandwidth is limited because the cost per bit is relatively high compared to low-speed memory like disks [Costello98]. The error rates are usually low and tend to occur by the byte so a SEC/DED coding scheme for each byte provides sufficient error protection. Error coding must be fast in this situation because high throughput is desired. SEC/DED codes are extremely simple and do not cause a high coding delay.
Cyclic Redundancy Check (CRC) codes are a special subset of linear block codes that are very popular in digital communications. CRC codes have the cyclic shift property; when any code word is rotated left or right by any number of bit digits, the resulting string is still a word in the code space [Wells99]. This property makes encoding and decoding very easy and efficient to implement by using simple shift registers. The main drawback of using CRC codes is that they have only error detecting capabilities. They cannot correct for any errors in the data once detected at the destination, and the data must be transmitted again to receive the message. For this reason, CRC codes are usually used in conjunction with another code that provides error correction. If CRC codes are the only ones used for an application, the raw BER of the channel is usually extremely low, and data is not time-critical. They are good for magnetic and optical storage, where a simple retransmit request to correct bit errors is feasible.
Convolutional codes are generally more complicated than linear block codes, more difficult to implement, and have lower code rates (usually below 0.90), but have powerful error correcting capabilities. They are popular in satellite and deep space communications, where bandwidth is essentially unlimited, but the BER is much higher and retransmissions are infeasible.
Convolutional codes are more difficult to decode because they are encoded using finite state machines that have branching paths for encoding each bit in the data sequence. A well-known process for decoding convolutional codes quickly is the Viterbi Algorithm. The Viterbi algorithm is a maximum likelihood decoder, meaning that the output code word from decoding a transmission is always the one with the highest probability of being the correct word transmitted from the source.
Error coding is a method of achieving fault tolerant computing, but also has ties embedded communications and factors into designing dependable real-time systems.
The following ideas are the important ones to take away from reading about this topic: