[Download postscript version]

Hash visualization requirements

For the security of the hash visualization, Random Artneeds to satisfy the near-one-way requirements listed in section 2.2. We can achieve the hash function one-way properties by hashing the input string with a cryptographically secure hash function, such as SHA-1 [10], to seed a cryptographically secure random number generator, such as Blum-Blum-Shub [5]. Hence, we can achieve the pre-image-resistance property. But the difficulty is to achieve collision-free, due to the properties of the image generation. First, it is easy to see that many different trees generate identical images. As an example we mention the commutative property of addition or multiplication, where the image remains invariant when swapping sub-trees of those operators. In addition, certain constructs can ``destroy'' randomness: As an example we consider a construct such as If x 0.999 then A else B. Since $x\; \in [0,1]$, the condition is always true if the image is smaller than 1000x1000 pixels, hence the subtree in the else case is never evaluated. In addition, the hash visualization properties take the human factor into account and therefore two images $I$₁ and $I$₂ collide if they are near $(I$₁ I₂). Due to these issues, we could not formally prove that the images generated by Random Artsatisfy the hash visualization requirements.

Instead, we propose to perform experiments to empirically estimate the difficulty to generate an image collision. With the assumption that all images produced by Random Artare equally likely, our approach is to pick random seeds and count how many perceptually different images can be generated. To perform the actual counting, we make use of a statistical estimation method, based on the birthday paradox. The birthday paradox basically expresses that if we draw random samples out of a uniform distribution with $N$ distinct values, we start seeing duplicates after approximately $N$ drawings. The name birthday paradox comes from the fact that we expect with a 50% probability, to have two people with the same birthday as soon as we have more than 24 people.

We can apply this technique to estimate the total number of images in the following way. First, we assume that every image is equally likely. We can then compute the probability that a certain number of collisions were encountered, given the total number of different images $N$, the number of images generated $n$, and the number of collisions $m$. An upper bound for the probability is: $P(N,n,m)\; \le \; n-1m\{N!Nn-m-1(N-n+m+1)!\}(\{n-mN\})m$. But since the user study will reveal for each sample $s$_i $(1\; \le i\; \le n)$ whether it is new or a collision, we can compute the precise probability:

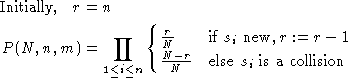
Since only $n$ and $m$ are known from the user study, we can compute $N$ through a maximum-likelihood estimation: which value of $N$ maximizes the probability? It is generally known as a good rule of thumb that squaring the number of samples after the first collision, is a good estimate for $N$.

Notice that Random Artis only a prototypical solution, and hence, might not be the final answer for hash visualization.